微软出品的经典地图匹配算法

马尔科夫模型

马尔科夫过程

马尔科夫过程是一类随机过程，他的原始模型是马尔科夫链。该过程具有如下特性：在目前已知的状态下，它未来的状态不依赖于过去的状态。在现实世界中，有很多过程都是马尔科夫过程，如微粒的布朗运动，传染病受感染的人数，车站的候车人数等。

马尔科夫链

马尔科夫链是数学中具有马尔科夫性质的离散时间随机过程。在该过程中，在给定当前知识或信息情况下，过去对于预测未来的状态是无关的，这种性质叫做无后效性。
时间和状态都是离散的马尔科夫过程称为马尔科夫链。假设状态序列为… xt−2x_{t-2},xt−1x_{t-1},xtx_{t},xt+1x_{t+1},xt+2x_{t+2}…，由马尔科夫链定义可知，时刻xt+1x_{t+1}的状态只和xtx_{t}有关，也就是：

P(xt+1∣…,xt−2,xt−1,xt)=P(xt+1∣xt)P(x_{t+1}|…, x_{t-2},x_{t-1},x_{t}) = P(x_{t+1}|x_t)

上面那个恒等式被称作马尔科夫性质。

马尔科夫模型

马尔科夫模型是一种统计模型，广泛引用在语音识别，词性自动标注，概率文法，地图道路匹配等领域。马尔科夫模型由三个要素组成。

状态
初始状态：在初始时间的各个状态的概率
状态转移矩阵：每种状态转移的概率

隐式马尔科夫模型模型

相比马尔科夫模型来讲，隐式马尔科夫模型中的状态不是明确确定的，新增了一个观测状态的概念，一个实际状态可能对应多个观测状态，实际状态到观测状态的概率称为观测概率或发射概率。下图展示隐式马尔科夫模型的联合概率分布。
pic
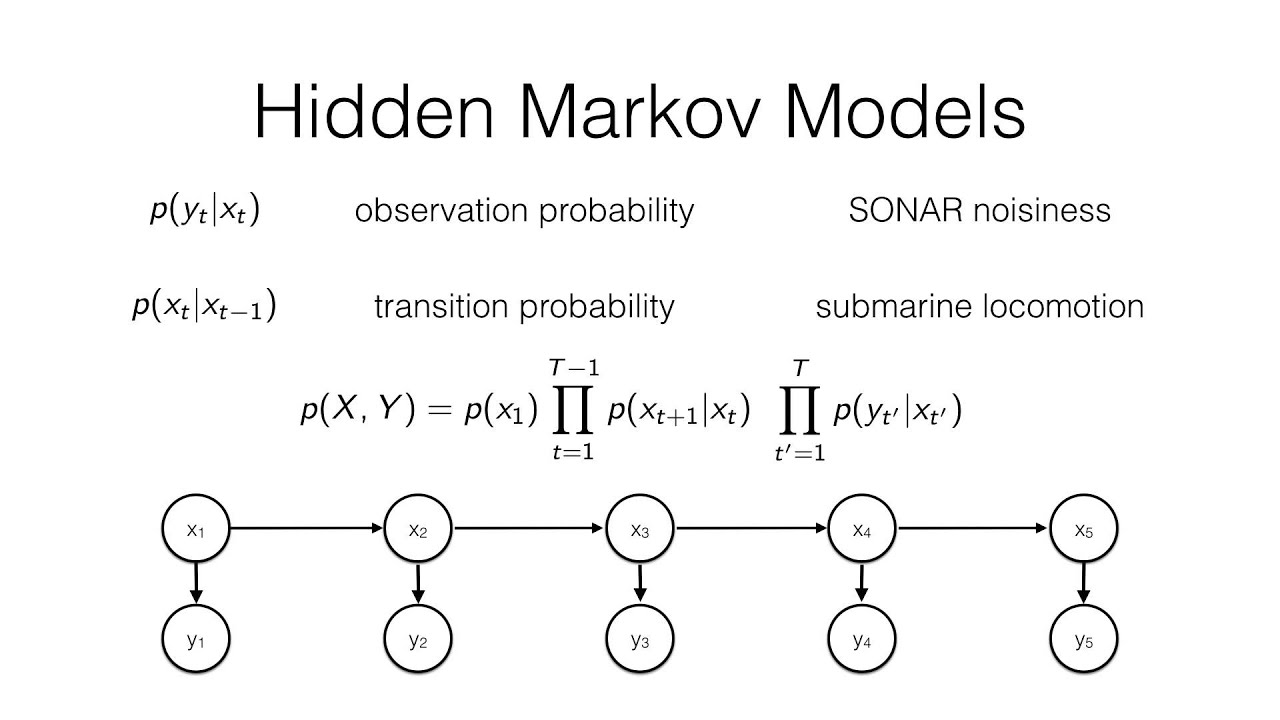
隐式马尔科夫模型模型包含以下五要素

实际状态
观测状态
初始状态概率分布
转移概率：实际状态之间转移概率
发射概率：实际状态被观测为特定观测状态的概率，也可以称为观测概率

隐式马尔科夫模型的一个应用是根据一系列观测状态来推测最有可能的实际状态。该问题可以用维特比算法来解决。

维特比算法

维特比算法(Viterbi algorithm)是一种动态规划算法，它用于寻找最有可能观测事件序列的维特比路径(隐含状态序列)，特别是在马尔科夫信息源上下文和马尔科夫模型中。
维特比算法的思想是从开始状态之后没走一步就记录下到达该状态所有路径的概率最大值，然后以此最大值为基准继续向后推进。显然，如果这个最大值都不能使该状态称为最大似然路径上的节点的话，那些小于它的概率值以及对应的路径就更没可能。下图摘自wikipedia，展示Viterbi算法的计算过程。
pic

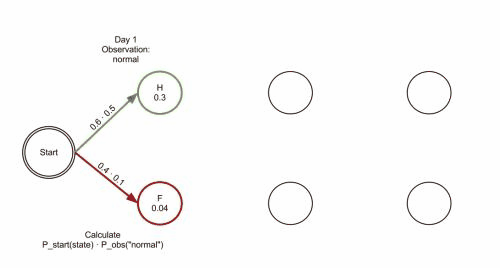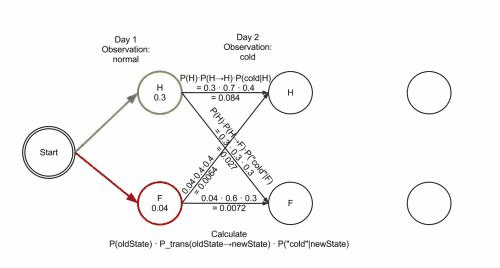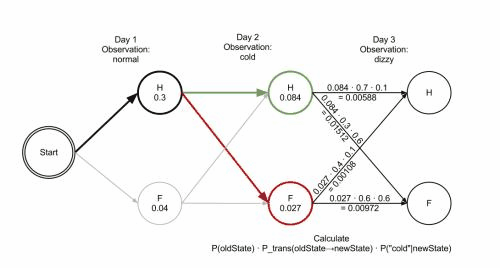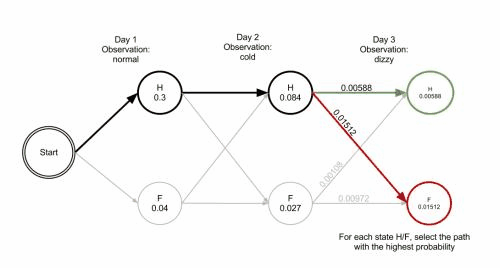
Map-Matching问题描述

Map-Matching 需要解决的问题是由GPS模块收集的经纬度序列转化为落在实际路网中的经纬度序列。产生此问题的原因是GPS模块上报的经纬度序列中含有大量噪声。

隐式马尔科夫模型实现Map-Matching

针对上面描述的问题，我们认为GPS模块中上报的每个经纬度点为一个观测状态。真实轨迹中落在真实道路上的经纬度点为隐藏状态。这个问题我们可以认为是一个典型的隐式马尔科夫模型，在此模型上应用维特比算法就可以解决map-matching问题。除了观测状态以及隐藏状态外，我们还需要建模发射概率以及转移概率 。下面介绍发射概率以及转移概率的计算方法

发射概率

针对一个观测的经纬度点，可能的实际轨迹点我们通过使用Rtree或者kdtree等空间索引搜索出观测点附近的道路，观测经纬度点到道路的投影点就是可能的实际点，实际点到观测点的直线距离服从均值为0，标准差为σzσ_z的高斯分布。
pic
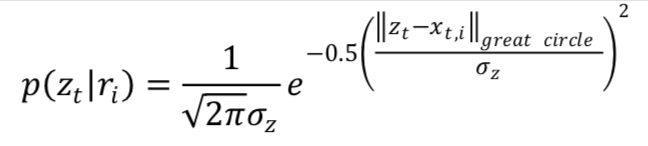
σzσ_z 代表GPS的定位精度。
pic

转移概率

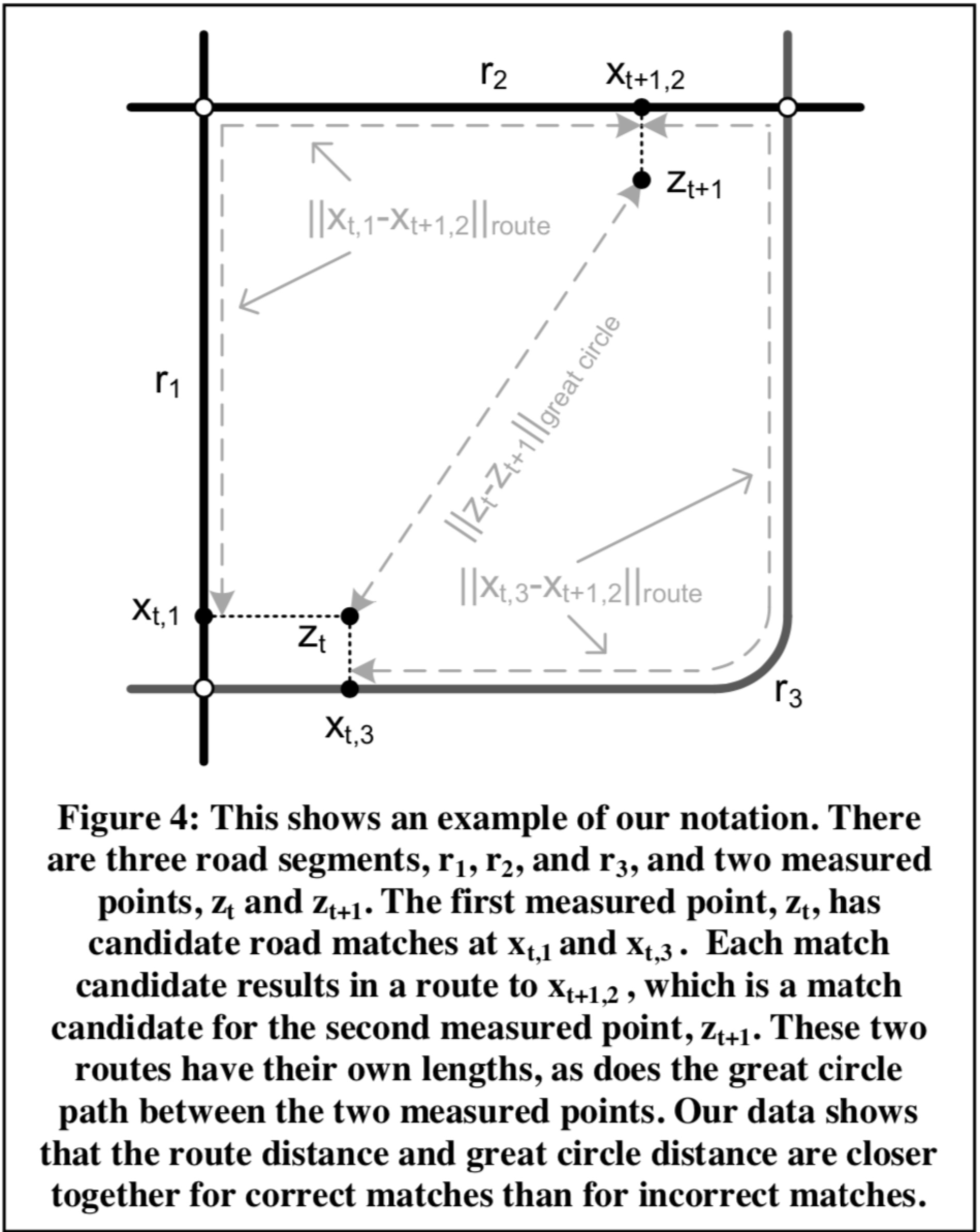
转移概率根据当前时间和上一时间观测点之间直线距离和实际点的导航绝对距离差来计算。通过绘制柱状图得知此绝对距离差服从均值为β的指数分布，如下图所示：
pic
pic
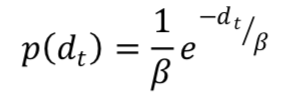
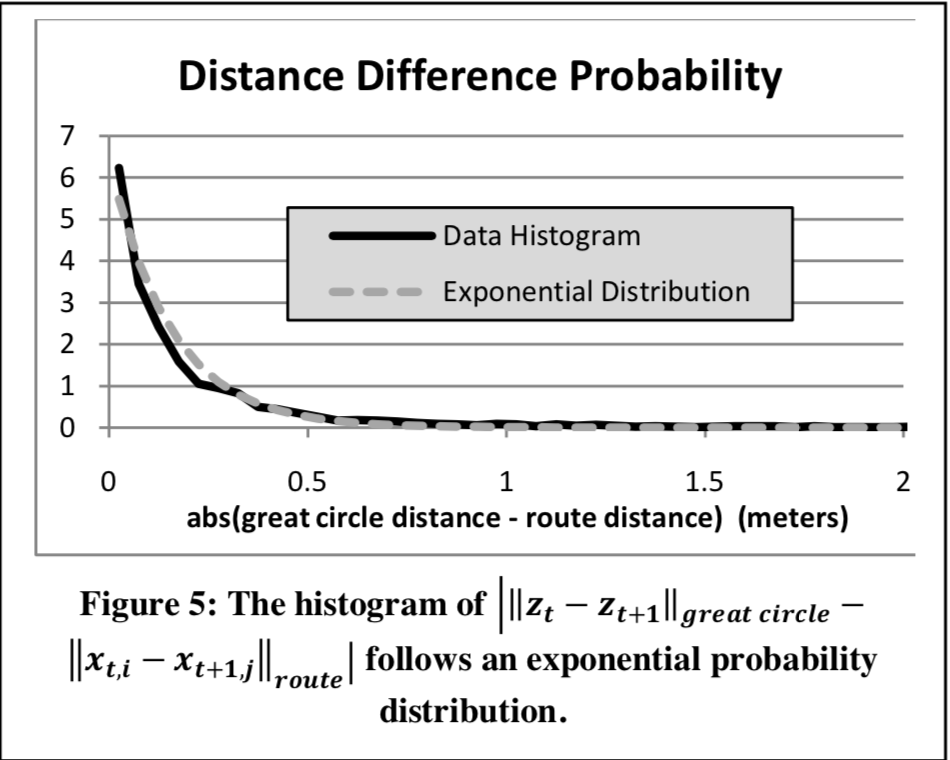
β的估算方法如下：
pic

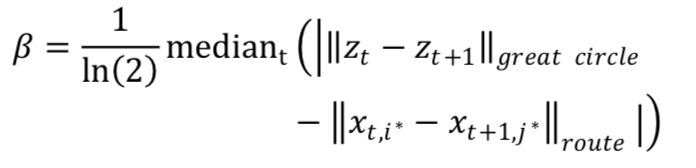
REFERENCE

《机器学习》- 周志华
Hidden Markov Map Matching Through Noise and Sparseness