经典路径规划算法之一

Floyd算法是为了解决有向图中所有点对之间最短距离问题。

算法描述

Floyd算法属于动态规划算法，算法的思路是我们以遍历每个节点k 作为中间节点，对于每个起终点对(i， j)来说，有以下两种可能情况：

  1. k 不是从i 到 j 最短路径的中间节点，不更新 dist[i][j]
  2. k 是从i 到 j 最短路径的中间节点，将dist[i][j] 更新为 dist[i][k] + dist[k][j]

示例

我们以以下有向图为例：
pic
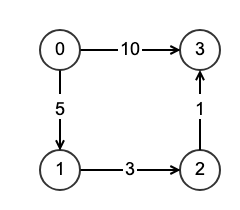
我们使用一下二维数组表示该图

vector<vector<int>> graph = {{0, 5, INT_MAX, 10},
                             {INT_MAX, 0, 3, INT_MAX},
                             {INT_MAX, INT_MAX, 0, 1},
                             {INT_MAX, INT_MAX, INT_MAX, 0}};

C++实现

/*************************************************************************
    > File Name: floyd.cpp
    > Author: ce39906
    > Mail: ce39906@163.com
    > Created Time: 2019-05-17 11:05:58
 ************************************************************************/
#include <vector>
#include <iostream>
#include <iomanip>

using namespace std;

void printResult(const vector<vector<int>>& dist)
{
    cout << "The following matrix shows the shortest distances "
            "between each pair of vertices" << endl;
    const int n = dist.size();
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < n; j++)
        {
            if (dist[i][j] == INT_MAX)
            {
                cout << setw(10) << "INT_MAX";
            }
            else
            {
                cout << setw(10) << dist[i][j];
            }
        }

        cout << endl;
    }
}

void floydWarshall(const vector<vector<int>>& graph)
{
    const int v = graph.size();
    vector<vector<int>> dist = graph;
    // main dp loop
    for (int k = 0; k < v; k++)
    {
        for (int i = 0; i < v; i++)
        {
            if (dist[i][k] == INT_MAX)
            {
                continue;
            }

            for (int j = 0; j < v; j++)
            {
                if (dist[k][j] == INT_MAX)
                {
                    continue;
                }

                if (dist[i][k] + dist[k][j] < dist[i][j])
                {
                    dist[i][j] = dist[i][k] + dist[k][j];
                }
            }
        }
    }

    printResult(dist);
}

int main()
{
    vector<vector<int>> graph = {{0, 5, INT_MAX, 10},
                                 {INT_MAX, 0, 3, INT_MAX},
                                 {INT_MAX, INT_MAX, 0, 1},
                                 {INT_MAX, INT_MAX, INT_MAX, 0}};
    floydWarshall(graph);

    return 0;
}

运行结果

编译

g++ --std=c++11 floyd.cpp -o floyd

运行结果

pic